We next consider the case of the trajectory of a light ray in
a spherically symmetric static gravitational field.
The calculation is essentially the same as that given in
the last section, except that light rays travel on null
geodesics, so that 
. The differential equation we need
to solve is therefore
In the limit of Special Relativity, the last term vanishes and the equation becomes
The general solution can be written in the form
where b is the closest approach to the origin [ or impact parameter, see Figure 8.2 ].
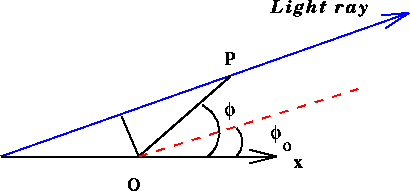
Figure 8.2: Deflection of light ray
This is the equation of a straight line as 
goes
from 
to 
. The straight line motion is
the same as predicted by Newtonian theory.
We again solve the General Relativity problem by taking the general solution to be a perturbation of the Newtonian solution:
where we have taken 
for convenience. It follows
that the equation for 
is:
This equation can be solved by trying a particular integral of the form
This gives [ Assignment 7 ]
so the full solution is
Let us now calculate the deflection of a light ray from a star which just grazes the sun [ see Figure 8.3 ].
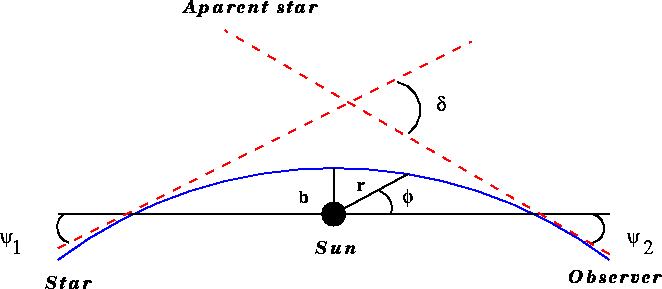
Figure 8.3: Diagram showing the total deflection
When 
, 
, so
at the asymptotes 
and 
, and
taking 
we get:
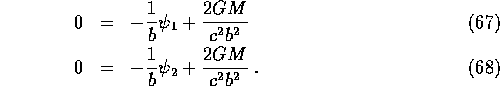
The total deflection is 
:
This works out to be about 1.75'' and was confirmed by Eddington in 1919 during a solar eclipse.
Another beautiful example of the bending of light is the gravitational lens. Take the example of a Quasar directly behind a galaxy in our line of sight.
The distance of closest approach corresponds to an angle
Now from the diagram [ see Figure 8.4 ] above we have
since both 
and 
are small. It follows that
the impact parameter can be written as
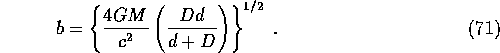
Figure 8.5: Einstein ring lensing event
So the image of the quasar appears as a ring which subtends an angle
